class: center, middle, inverse, title-slide # Задача классификации ## Логистическая регрессия, K-nn ### Konstantin Zaitsev <br/> Summer school 2017 ### 1/08/2017 --- background-image: url(MachineLearningDiagram.png) background-size: cover --- # Задача классификации Имеется множество объектов, разделенных некоторым образом на **классы**. Для каких-то объектов известно к какому классу они относятся (выборка), для остальных -- нет. Требуется построить алгоритм, способный классифицировать произвольный объект из исходного множества --- ## Задача классификации: формально - Каждый объект `\(x\)` описывается набором признаков `\(x_1, x_2, \dots , x_m\)`, а также известно значение зависимой переменной, которую мы пытаемся предсказать `\(y\)`. - ** `\(y\)` -- теперь дискретная переменная, которая описывает класс объекта:** $$ y \in Y:Y = \{c_1, c_2, ..., c_k\} $$ - Тогда все объекты можно представить матрицей `\(X\)` размера `\(n \times m\)`, где `\(n\)` -- количество объектов, а `\(m\)` -- количество признаков. -- Задача классификации заключается в нахождении зависимости дискретной переменной переменной `\(y\)` от вектора признаков `\((x_1, \dots , x_m)\)`: $$ f(x_1, \dots, x_m) = f(x) \sim y $$ -- Задача классификации -- задача нахождения функции `\(f\)`. --- ## Примеры использования задачи классификации - Диагностика заболеваний: два класса -- болен / не болен - Письма в почтовом ящике: два класса -- спам / не спам - Iris dataset: три класса описывающие различные виды растений - Классификация патогенных / непатогенных бактерий - Классификация изображений --- ## IRIS dataset ```r data("iris") summary(iris) ``` ``` ## Sepal.Length Sepal.Width Petal.Length Petal.Width ## Min. :4.300 Min. :2.000 Min. :1.000 Min. :0.100 ## 1st Qu.:5.100 1st Qu.:2.800 1st Qu.:1.600 1st Qu.:0.300 ## Median :5.800 Median :3.000 Median :4.350 Median :1.300 ## Mean :5.843 Mean :3.057 Mean :3.758 Mean :1.199 ## 3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800 ## Max. :7.900 Max. :4.400 Max. :6.900 Max. :2.500 ## Species ## setosa :50 ## versicolor:50 ## virginica :50 ## ## ## ``` --- ## IRIS dataset: беглый взгляд ```r library(ggplot2) ggplot(iris, aes(x=Sepal.Length, Petal.Length, color=Species)) + geom_point() + theme_bw() ``` <img src="lecture2_files/figure-html/unnamed-chunk-2-1.png" width="100%" /> --- ## Метод К ближайших соседей K-nn = K nearest neighbors = K ближайших соседей Очень простой метод классификации: - Пускай про какие-то объекты известны их классы - Чтобы классифицировать объект неизвестного класса достаточно посмотреть на `\(k\)` ближайших соседей этого объекта с известным классом - Выбрать тот класс, который наиболее представлен среди соседей -- - Профит! --- ## K-nn, K = 3 .tofit[] --- count: false ## K-nn, K = 3 .tofit[] --- count: false ## K-nn, K = 3 .tofit[] --- count: false ## K-nn, K = 3 .tofit[] --- count: false ## K-nn, K = 3 .tofit[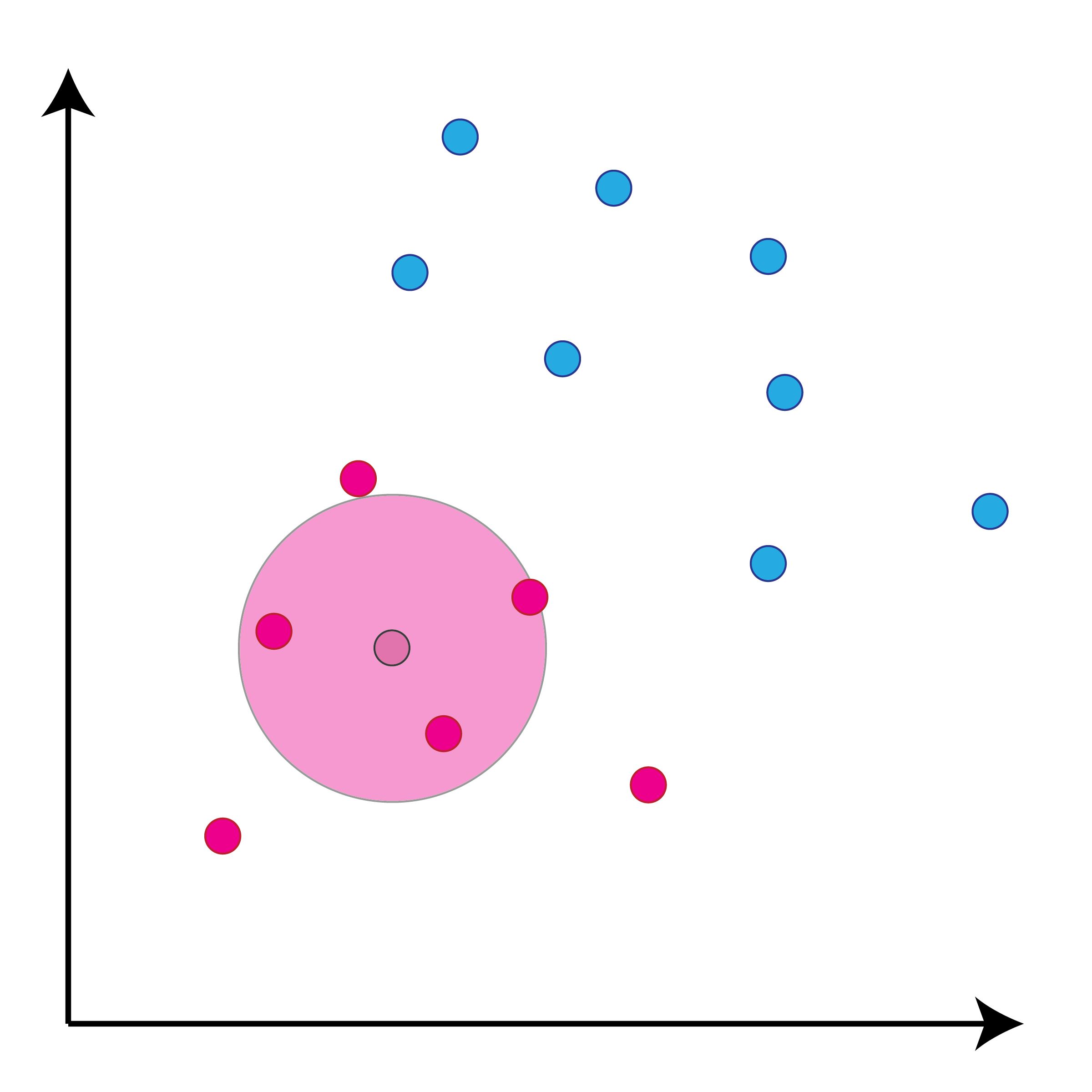] --- count: false ## K-nn, K = 3 .tofit[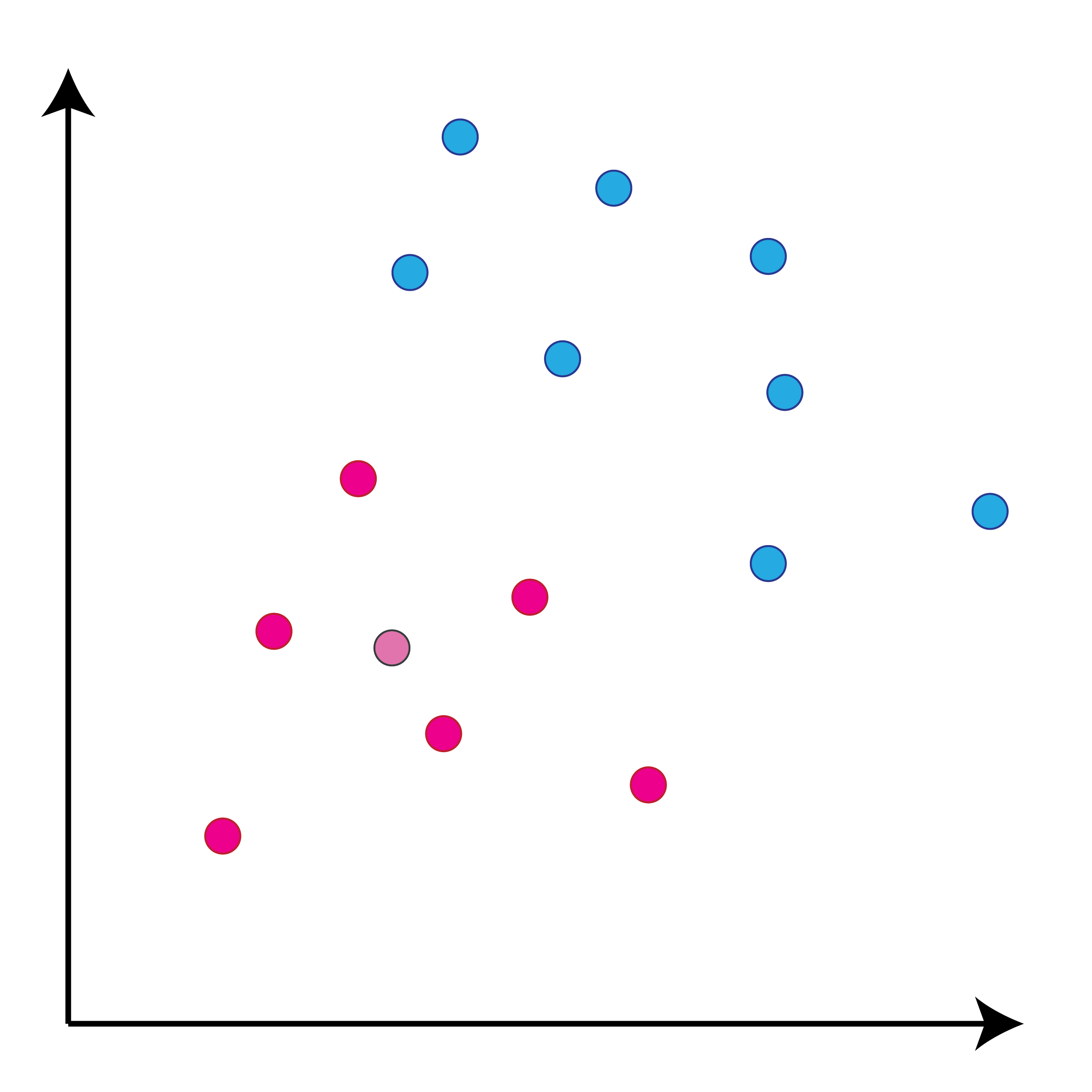] --- count: false ## K-nn, K = 3 .tofit[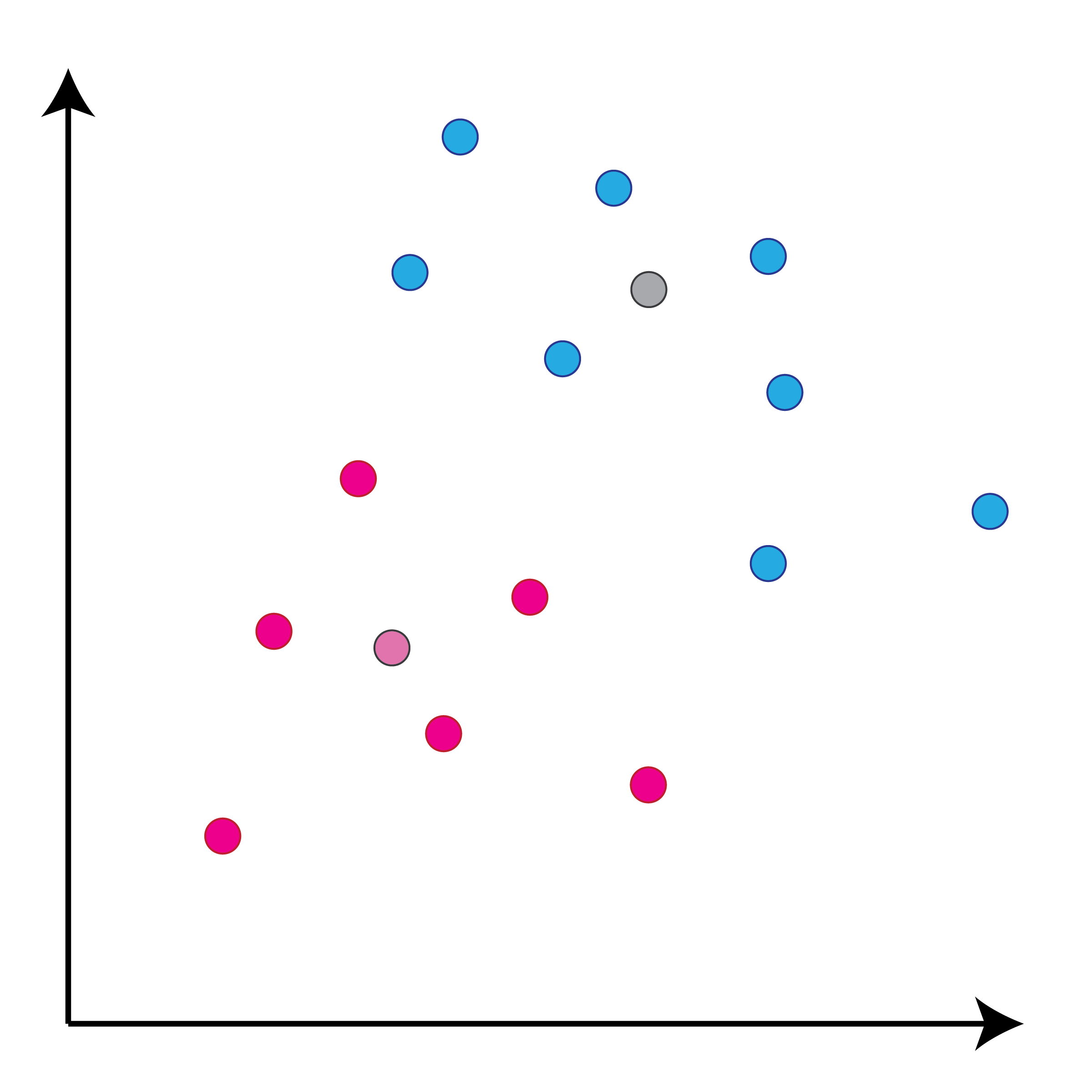] --- count: false ## K-nn, K = 3 .tofit[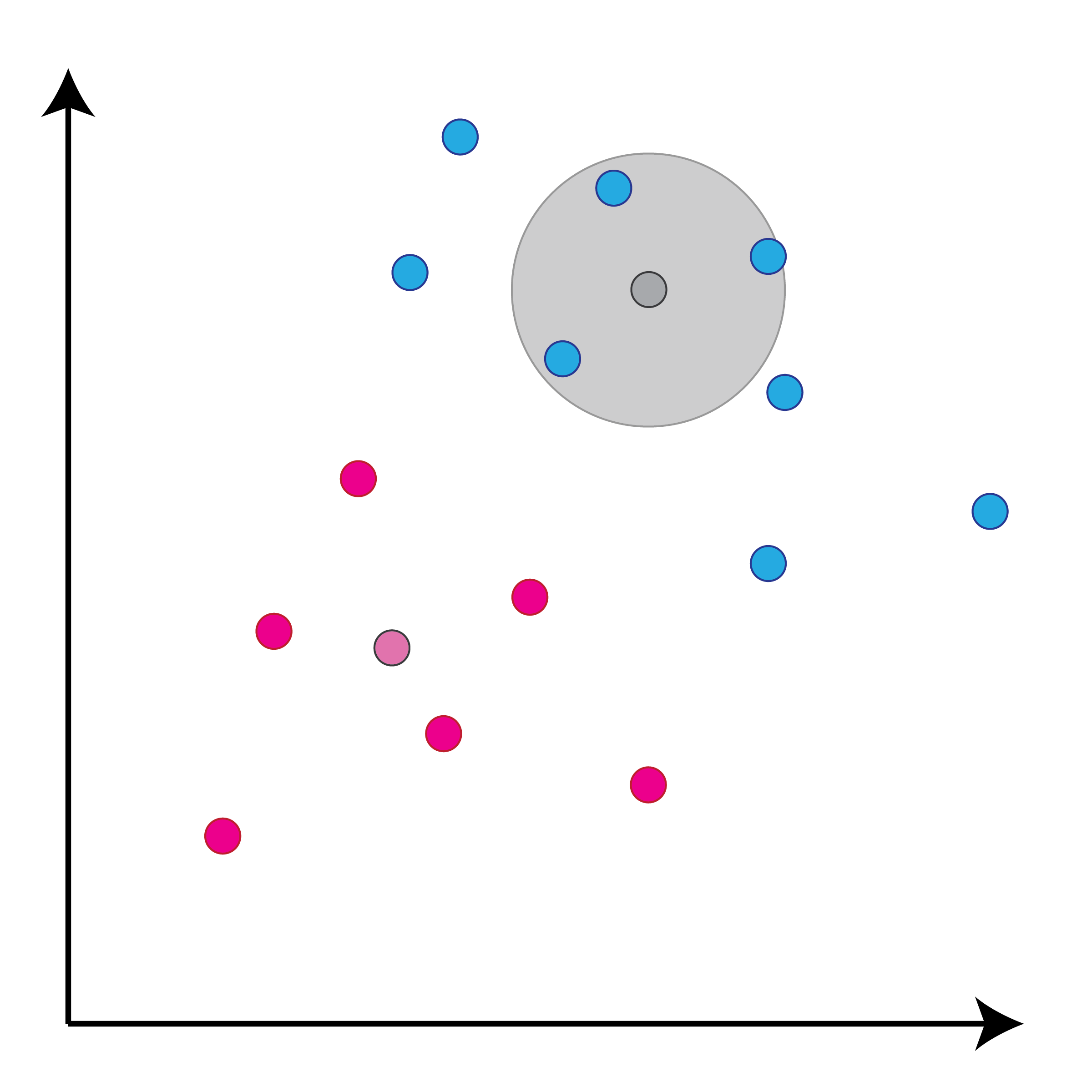] --- count: false ## K-nn, K = 3 .tofit[] --- count: false ## K-nn, K = 3 .tofit[] --- count: false ## K-nn, K = 3 .tofit[] --- count: false ## K-nn, K = 3 .tofit[] --- count: false ## K-nn, K = 3 .tofit[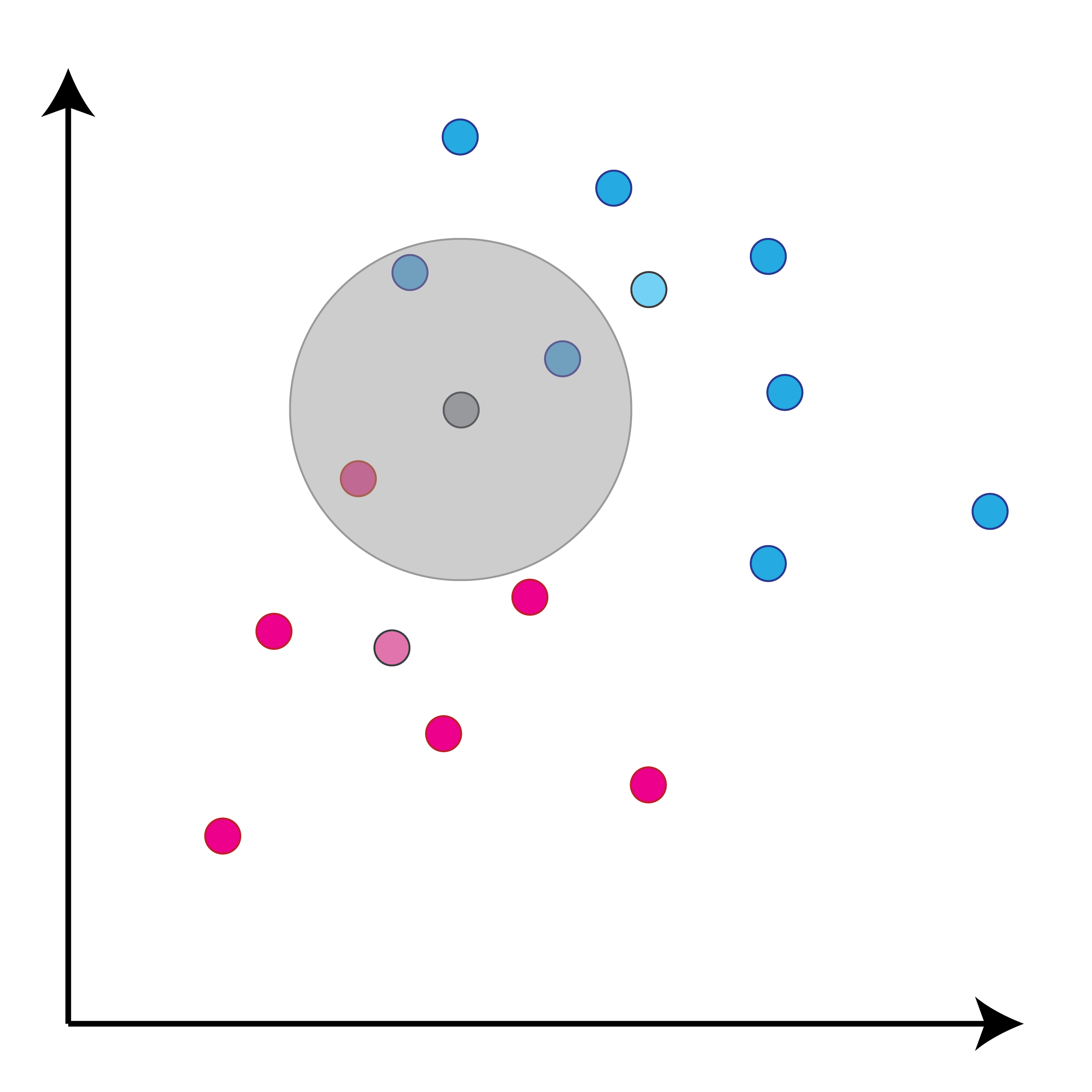] --- count: false ## K-nn, K = 3 .tofit[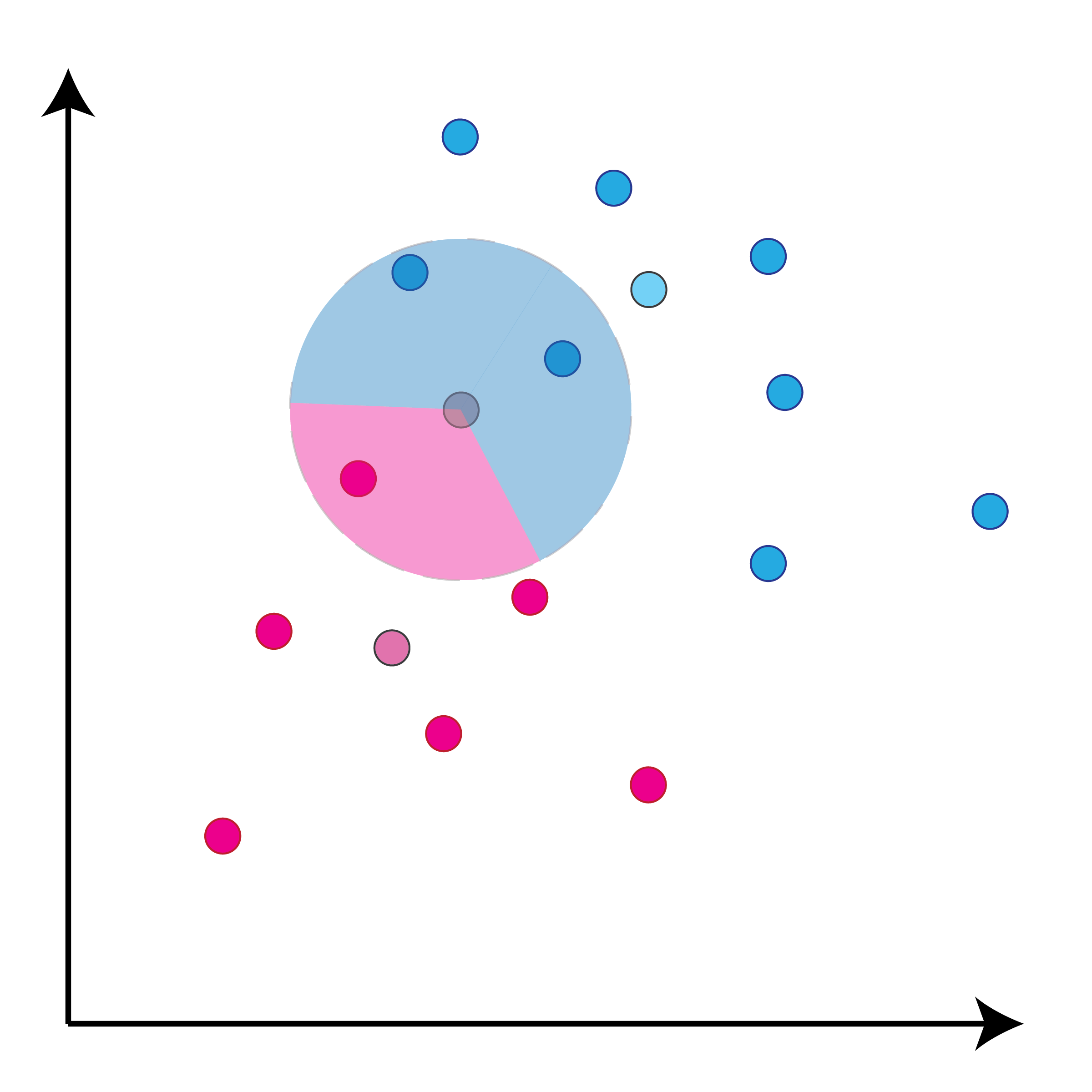] --- count: false ## K-nn, K = 3 .tofit[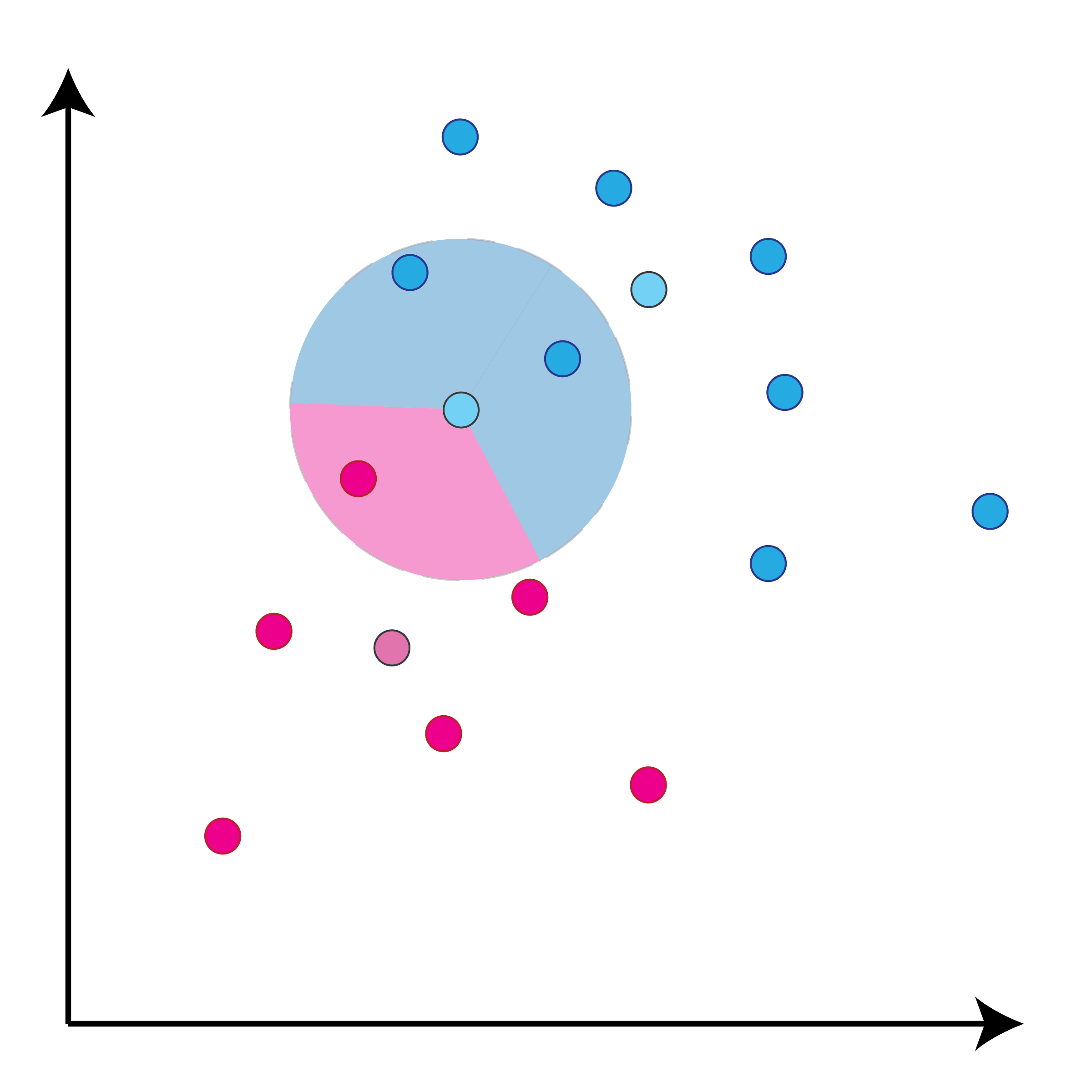] --- ## IRIS dataset: разбили на train/validation ```r set.seed(1) training <- sample(1:150, 120) validation <- (1:150)[-training] train <- iris[training, ] valid <- iris[validation, ] ``` --- ## IRIS dataset: разбили на train/validation ```r library(ggplot2) ggplot(train, aes(x=Sepal.Length, Petal.Length, color=Species)) + geom_point() + theme_bw() + geom_point(data=valid, mapping = aes(color=NA)) ``` <img src="lecture2_files/figure-html/unnamed-chunk-4-1.png" width="100%" /> --- ## K-nn on iris data ```r library(class) ``` ``` ## Warning: package 'class' was built under R version 3.3.3 ``` ```r prediction <- knn(train[, 1:4], valid[, 1:4], train$Species, k=5) prediction ``` ``` ## [1] setosa setosa setosa setosa setosa setosa ## [7] setosa setosa setosa setosa versicolor versicolor ## [13] versicolor versicolor versicolor versicolor versicolor versicolor ## [19] virginica virginica virginica virginica virginica virginica ## [25] virginica virginica virginica virginica virginica virginica ## Levels: setosa versicolor virginica ``` --- ## K-nn on iris data ```r table(valid$Species, prediction, dnn=c("actual", "predicted")) ``` ``` ## predicted ## actual setosa versicolor virginica ## setosa 10 0 0 ## versicolor 0 8 0 ## virginica 0 0 12 ``` --- ## K-nn Плюсы: - Просто, быстро и понятно - Несложно сделать из этого регрессию (брать взвешенное среднее соседей) Минусы: - Нужно чтобы данные можно было представить как точки в многомерном Евклидовом пространстве - Нужно чтобы расстояние между этими точками действительно отражало "похожесть" и "непохожесть" объектов --- ## Бинарная классификация Важнейшая подзадача задачи классификации. Наше множество классов Y представлено лишь двумя классами: $$ Y = \{c_1, c_2\}$$ это может быть положительная/отрицательная диагностика заболевания, определение спам/не спам и другие типы. --- ## Серьезные данные ```r library(foreign) data <- read.arff("diabetes.arff.txt") head(data) ``` ``` ## preg plas pres skin insu mass pedi age class ## 1 6 148 72 35 0 33.6 0.627 50 tested_positive ## 2 1 85 66 29 0 26.6 0.351 31 tested_negative ## 3 8 183 64 0 0 23.3 0.672 32 tested_positive ## 4 1 89 66 23 94 28.1 0.167 21 tested_negative ## 5 0 137 40 35 168 43.1 2.288 33 tested_positive ## 6 5 116 74 0 0 25.6 0.201 30 tested_negative ``` --- ## Как оценивать успешной бинарной классификации  `\(Precision = \frac{TP}{TP + FP}\)` `\(Recall\ (TPR) = \frac{TP}{TP + FN}\)` `\(Accuracy = \frac{TP + TN}{TP + FP + FN + TN}\)` `\(FPR = \frac{FP}{FP + TN}\)` --- ## Логистическая регрессия .large[ - Метод "регрессии", когда зависимая переменная `\(y\)` описывается дискретным множеством классов. ] -- .large[ - Логистическая регрессия очень часто применяется в контексте бинарной классификации. ] -- .large[ - Почему регрессия? ] --- ## Логистическая регрессия 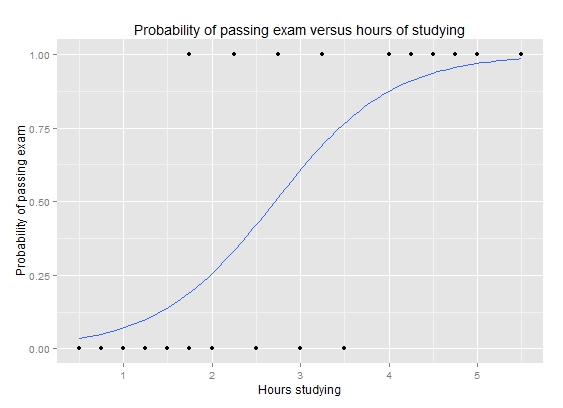 --- ## Как всегда: делим выборку на train/validation ```r set.seed(1) validation <- sample(1:nrow(data), nrow(data) %/% 5) training <- (1:nrow(data))[-validation] train <- data[training, ] valid <- data[validation, ] ``` --- ## Обучим нашу модель, и проверим, как она может предсказывать ```r model <- glm(class ~ ., family = binomial, data=train) prediction <- predict(model, valid, type="response") prediction <- ifelse(prediction > 0.5, "tested_positive", "tested_negative") table(valid$class, prediction) ``` ``` ## prediction ## tested_negative tested_positive ## tested_negative 87 14 ## tested_positive 17 35 ``` --- ## ROC-кривая ROC-кривая (ROC -- reciever operator characteristic) -- график для оценки качества бинарной классификации, отображает соотношение между долей объектов, верно классифицированных, как несущие признак, и долей объектов, верно классифицированных как ненесущие признак. .large[ Хотим строить зависимость TPR от FPR в зависимости от разного порога! ] --- ## ROC-кривая ```r library(pROC) probs <- predict(model, valid, type=c("response")) valid$probs <- probs g <- roc(class ~ probs, data = valid) ``` --- ## ROC-кривая ```r plot(g) ``` 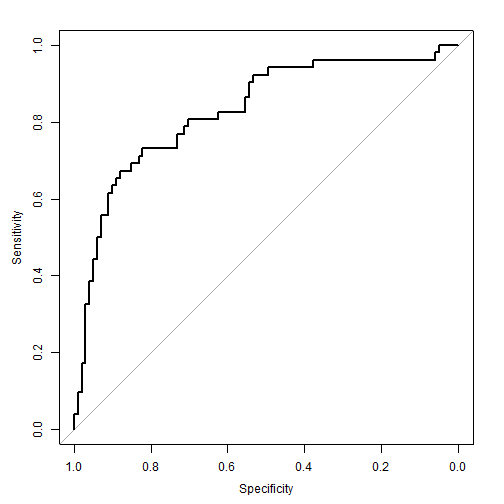<!-- -->